Matemáticas ludicas

¿Qué relación hay entre la música y las Matemáticas?

Introducción

Es común escuchar que “hay Matemática en la Música porque cuando se abre una partitura ésta está llena de numeritos”, es decir, de los números del compás y las digitaciones. Obviamente esta observación es muy simple. Se dice que hay Matemática en la Música, que la Música y la Matemática están muy relacionadas. Pero ¿hay Matemática en la Música? ¿Están relacionadas? ¿Qué relación existe entre la Música y la Matemática?

Hay desde luego similitudes innegables como que ambas tienen algo de mágico, son tan abstractas que parecen pertenecer a otro mundo y sin embargo tienen gran poder en este mundo, la música afecta al que escucha y las matemáticas tienen múltiples aplicaciones prácticas. Una parte de las matemáticas estudia los números, sus patrones y formas y estos elementos son inherentes a la ciencia, la composición y la ejecución de la música.

Leibniz describe a la Música como "un ejercicio inconsciente en la Aritmética". Esta afirmación quizás se podría justificar sobre la base de que el músico intérprete cuenta los tiempos del compás cuando comienza a estudiar una obra pero después de un tiempo de tocarla, ya no está contando conscientemente sino que deja fluir la magia de la Música. Sin embargo casi todos los "elementos externos" de la Música se definen numéricamente: 12 notas por octava; compás de 3/4, 7/8,...; 5 líneas en el pentagrama; n decibeles; semitono de raíz duodécima de dos; altura de 440 hz; lo horizontal y lo vertical en la textura musical; arriba y abajo en la escala; etc.

En tiempos de la antigua Grecia, la Música no sólo se consideró como una expresión artística de las Matemáticas sino que su estudio y análisis estuvo siempre ligado a la Teoría de los Números y a la Astrología. De hecho, para los griegos la teoría matemática de la música formaba parte de una teoría general conocida como la Armonía del Cosmo. Pitágoras y sus discípulos, Platón, Aristógenes, Aristóteles y Claudio Ptolomeo fueron algunos de los filósofos y astrólogos más relevantes que profundizaron en los intervalos musicales como fuente de nociones matemáticas y de importantes extrapolaciones científicas y cosmológica

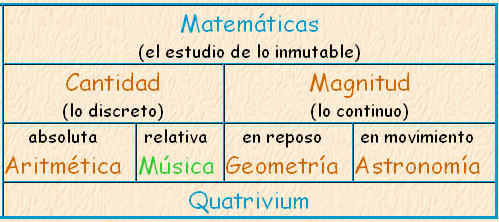
En la Edad Media la Música estaba agrupada con la Aritmética, la Geometría y la Astronomía en el Cuadrivio. La Música no se consideraba un arte en el sentido moderno sino una ciencia aliada con la Matemática y la Física (la Acústica). Matemáticas un poco más elevadas se utilizaron en el cálculo de intervalos, el cual requería el uso de logaritmos, y los problemas del temperamento requerían del uso de fracciones continuas.

La música cambia su textura y carácter según el lugar y la época. Puede ser cristalina o densa, sentimental o explosiva. Por su parte, las matemáticas son directas, nunca alteran su carácter. La música se crea a partir de algo físico, instrumentos de todo tipo de materiales la producen. Las matemáticas son, sobre todo, abstracciones que no necesitan ni siquiera papel y lápiz. El mundo actual no podría concebirse sin ellas, ¿cómo haber llegado a la tecnología y a todos los inventos modernos sin las matemáticas?

La música está cargada de emociones, es alegre o triste, suave o agresiva, puede ser espiritual, estética, religiosa pero no podemos hablar de un teorema “triste” o de una demostración “agresiva”.

Tanto el matemático como el músico se encuentran ocupados resolviendo problemas o componiendo o interpretando, enseñando a alumnos sin detenerse a pensar que ambos están entregados a disciplinas que son paradigmas de lo abstracto.

Los Pitagóricos

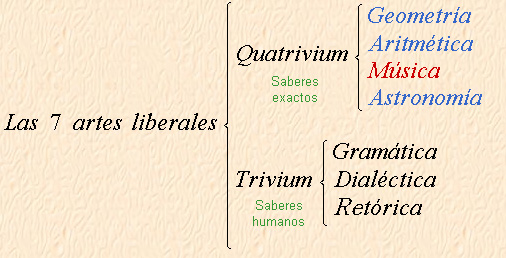
En la época de los antiguos griegos, Pitágoras y los pitagóricos (siglo VI a.C) fueron los primeros en desarrollar una división del curriculum llamado quadrivium en donde la música se consideraba una disciplina matemática que manejaba relaciones de números, razones y proporciones. Esta división se mantuvo durante la Edad Media, por lo que era necesario el estudio de ambas disciplinas. El quadrivium (aritmética, música, geometría y astronomía), con el agregado del trivium (gramática, retórica y dialéctica), se convirtieron en las siete artes liberales, pero la posición de la música como un subconjunto de las matemáticas permaneció durante la Edad Media.

Las siete artes las dividían en “saberes exactos” (Quatrivium o Matemáticas) y “saberes humanos” (Trivium).

Pitágoras

Pitágoras de Samos (aproximadamente 582 adC - 507 adC) fue uno de los filósofos griegos más sabios de la Antigüedad. Fundó su propia escuela de pensamiento, la Escuela pitagórica, que afirmaba que la estructura del universo era aritmética y geométrica, a partir de lo cual las matemáticas se convirtieron en una disciplina fundamental para toda investigación científica. Como consecuencia, esta escuela se distinguió por estudiar y desarrollar los campos de las matemáticas, aritmética, geometría, astronomía y música entre otros.

Se dice que Pitágoras acuñó la palabra matemáticas, que significa “lo que es aprendido”. Él describe un sistema de ideas que busca unificar los fenómenos del mundo físico y del mundo espiritual en términos de números, en particular, en términos de razones y proporciones de enteros. Se creía que, por ejemplo, las órbitas de los cuerpos celestiales que giraban alrededor de la Tierra producían sonidos que armonizaban entre sí dando lugar a un sonido bello al que nombraban “la música de las esferas”.

Pitágoras estudió la naturaleza de los sonidos musicales. La música griega existía mucho antes, era esencialmente melódica más que armónica y era microtonal, es decir, su escala contenía muchos más sonidos que la escala de doce sonidos del mundo occidental.

Pitágoras consideraba que la esencia última de la realidad se expresaba a través de números. Los números eran el medio para percibir lo que de otra forma podría permanecer inalcanzable tanto para el intelecto como para los sentidos y como consecuencia trató de explicar matemáticamente la escala musical, que entonces era un gran misterio para los hombres. Estaba convencido de que los intervalos entre las notas de una octava podían ser representadas mediante números y en ello trabajó durante gran parte de su vida.

Como los pitagóricos veían que las propiedades y relaciones de la armonía musical están determinadas por los números y que todas las cosas están también conformadas según los números y que estos son lo primero en toda la naturaleza, pensaron que las relaciones de los números son las relaciones de todas las cosas y que el cielo entero es armonía y número.

La armonía de las esferas

Los pitagóricos fueron los primeros en definir el Cosmos como una serie de esferas perfectas que describían órbitas circulares. Pitágoras sostenía que los 7 planetas (Mercurio, Venus, La Tierra, Marte, Júpiter, Saturno, incluyendo el Sol), al describir sus órbitas, emitían unos sonidos, las notas musicales que creaban lo que él llamó la Armonía de las Esferas.

Para sus seguidores, los pitagóricos, las distancias entre los planetas -las esferas- tenían las mismas proporciones que existían entre los sonidos de la escala musical que eran considerados entonces como "armónicos" o consonantes. Cada esfera producía el sonido que un proyectil hace al cortar el aire. Las esferas más cercanas daban tonos graves, mientras que las más alejadas daban tonos agudos. Todos estos sonidos se combinaban en una hermosa armonía: la música de las esferas.

Cuenta la leyenda que cierto día, mientras Pitágoras paseaba por la calle escuchó unos golpeteos rítmicos que le llamaron poderosamente la atención. El ruido procedía de una herrería cercana hasta la cual el sabio de Samos se aproximó, atraído por la musicalidad de los golpes de los martillos sobre el yunque. Estuvo allí bastante rato, observando cómo trabajaban los herreros y cómo utilizaban sus herramientas, y se dio cuenta de que el sonido variaba según el tamaño de los martillos. Así Pitágoras descubrió la relación numérica entre las notas musicales, las mismas notas musicales que emitían los 7 planetas al girar alrededor de la Tierra.

No todos los pensadores de la antigüedad creyeron en la música de las esferas. Aristóteles, en su libro Del cielo, negó la existencia del universo sonoro propuesto por Platón: "La teoría de que el movimiento de las estrellas produce una armonía, es decir, sonidos que revelan una concordancia, a pesar de la gracia y la originalidad con que ha sido presentada, no por ello deja de ser falsa."

Sin embargo, las ideas que tuvieron la mayor influencia fueron los mitos de Platón. Así, pensadores como Cicerón, Arístides Quintilianus y Tolomeo apoyaron la teoría de la música de las esferas.

La creencia en algunas religiones de la existencia de ángeles en el universo junto con la música de las esferas dio origen a lo que se conoció como "música celeste". Esta era la música producida por los ángeles que se representó en muchas obras de arte de la Edad Media y del Renacimiento.

Además, hay que tener en cuenta que estas ideas fueron tomadas también en otros campos como la Astronomía: para su concepción del universo, Kepler se apoyó en los mitos de Platón y en el sistema de Copérnico que planteaba que el Sol era el centro en torno al cual giraban los planetas. Kepler postulaba que el modelo del universo estaba basado en la geometría: entre las órbitas de los seis planetas conocidos (Saturno, Júpiter, Marte, Tierra, Venus y Mercurio) estaban inscritos los cinco sólidos perfectos mencionados por Platón (cubo, tetraedro, dodecaedro, icosaedro y octaedro)

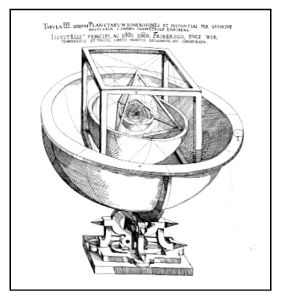
Kepler estudió cuidadosamente las órbitas de los planetas para establecer una relación entre el movimiento de estos cuerpos celestes con la teoría musical a la que se refirió como de Tolomeo, pero que había sido planteada por Gioseffo Zarlino. Finalmente, en su libro Harmonices Mundi, postuló que las velocidades angulares de cada planeta producían sonidos consonantes. Asumida esta creencia, escribió seis melodías: cada una correspondía a un planeta diferente. Al combinarse, estas melodías podían producir cuatro acordes distintos, siendo uno de ellos el acorde producido en el momento de la creación y otro el que marcaría el momento del fin del universo.

La teoría de Pitágoras

Para estos incipientes científicos, los números eran los verdaderos principios o esencias de las cosas, con lo que no es de extrañar que llegaran a una mística matemática que les llevara a considerar la armonía y la música como actividades purificadoras del alma. Esta creencia les llevó a entregarse a los estudios musicales, dando lugar al descubrimiento de que las proporciones entre las notas musicales y las longitudes de las cuerdas que las producen son isomorfas a proporciones existentes entre los números enteros. Así descubrirían los teoremas sobre cuerdas y se concentrarían en el estudio de las matemáticas motivados por la labor purificadora de las matemáticas al estar en relación con la música.

Fue Pitágoras quien descubrió que existía una relación numérica entre tonos que sonaban “armónicos” y fue el primero en darse cuenta de que la música, siendo uno de los medios esenciales de comunicación y placer, podía ser medida por medio de razones de enteros. Sabemos que el sonido producido al tocar una cuerda depende de la longitud, grosor y tensión de la misma. Entendemos que cualquiera de estas variables afecta la frecuencia de vibración de la cuerda. Lo que Pitágoras descubrió es que al dividir la cuerda en ciertas proporciones era capaz de producir sonidos placenteros al oído. Eso era una maravillosa confirmación de su teoría.

Pitágoras estaba influenciado por sus conocimientos sobre las medias (aritmética, geométrica y armónica) y el misticismo de los números naturales, especialmente los cuatro primeros (tetrakis). Había experimentado que cuerdas con longitudes de razones 1:2 (los extremos 1 y 2), 2:3 (media armónica de 1 y 2), y 3:4 (media aritmética de 1 y 2) producían combinaciones de sonidos agradables y construyó una escala a partir de estas proporciones. A estos intervalos los llamó diapasón, diapente y diatesaron. Hoy los llamamos octava, quinta y cuarta porque corresponden a esas notas de la escala pitagórica diatónica (do, re, mi, fa, sol, la, si, do). Los pitagóricos no sabían nada de ondas sonoras y de frecuencias. De hecho, la regla que establece que la frecuencia está relacionada con la longitud de la cuerda no fue formulada hasta el siglo XVII, cuando el franciscano fray Marin Mersenne definió algunas reglas sobre la frecuencia de una cuerda vibrando.

La razón por la cual encontramos a estos intervalos más agradables que otros tiene que ver con la física de la cuerda tocada. Cuando una cuerda de 36 cm se rasga, no sólo se produce una onda de 36 cm, sino que además se forman dos ondas de 18 cm, tres de 12, cuatro de 9, y así sucesivamente. La cuerda vibra en mitades, tercios, cuartos, etcétera. Y cada vibración subsidiaria produce “armónicos”, estas longitudes de onda producen una secuencia de armónicos, 1/2, 1/3, 1/4... de la longitud de la cuerda. Los sonidos son más agudos y mucho más suaves que el sonido de la cuerda completa (llamada “la fundamental”) y generalmente la gente no los escucha pero son los que hacen que los instrumentos musicales suenen diferentes entre sí. Ya que Do y Sol, a una distancia de quinta, comparten muchos de los mismos armónicos, estos sonidos se mezclan produciendo un resultado agradable.

Una de las enseñanzas clave de la escuela pitagórica era que los números lo eran todo y nada se podía concebir o crear sin éstos. Había un número especialmente venerado, el 10, al igual que la tetractys, siendo la suma de 1, 2, 3, y 4. La tetractys era el símbolo sagrado de los pitagóricos, un triángulo de cuatro hileras representando las dimensiones de la experiencia. 1 punto • 2 línea • • 3 plano • • • 4 sólido • • • •

En el caso de la música simbolizaba las proporciones entre las notas empezando por la proporción 1:2 para la octava. Los experimentos de Pitágoras con el monocordio llevaron a un método de afinación con intervalos en razón de enteros conocido como la afinación pitagórica. La escala producida por esta afinación se llamó escala pitagórica diatónica y fue usada durante muchos años en el mundo occidental. Se deriva del monocordio y de acuerdo con la doctrina pitagórica, todos sus intervalos pueden ser expresados como razones de enteros. Existen diferencias de afinación entre esta escala y la escala temperada usada actualmente.

Números y belleza eran uno. El mundo físico y el emocional podían ser descritos con números sencillos y existía una relación armónica entre todos los fenómenos perceptibles.

Las relaciones entre los sonidos

La notación modal y los modelos rítmicos

Como la polifonía medieval se iba haciendo cada vez más y más compleja, los compositores tenían que encontrar algún medio de indicar cómo encajaban las voces y los sonidos de los instrumentos musicales.

Lo que necesitaban era un sistema de notación que mostrara los valores relativos de las notas dentro de una única línea melódica. El desarrollo de ese sistema, fue una de las realizaciones más significativas de la escuela de Notre Dame.

Relaciones entre sonidos

En la música es muy importante la relación que existe entre la frecuencia de los distintos sonidos, a esta relación se le llama intervalo. Los intervalos musicales pueden medirse en términos de la relación de frecuencias de los sonidos, aunque en música reciben nombres propios cuya correspondencia física depende del tipo de escala utilizada.

Los más importantes, por su simplicidad y su importancia a la hora de construir la escala musical, son:

• La octava. Cuando la cuerda medía un medio del total, el sonido se repetía, pero más agudo. La octava es lo que correspondería a un salto de ocho teclas blancas del piano; o mejor dicho, una octava es la repetición de un sonido con una cuerda con la mitad de longitud, por tanto, otra nota armoniosa. Su frecuencia es doble.
  
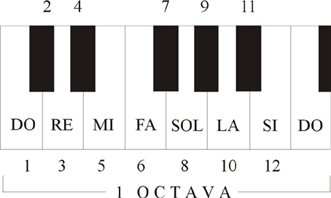
• La quinta es otro intervalo entre notas que se obtiene con una cuerda de largura dos tercios de la inicial. Su frecuencia es de tres medios del sonido inicial. Corresponde a un salto de cinco teclas blancas en un piano.
• La cuarta es, como las anteriores, otro intervalo entre notas que se obtiene con una cuerda de largura tres cuartos de la inicial. Su frecuencia es cuatro tercios de la nota inicial.

El siguiente esquema muestra un fragmento del teclado de piano, a cada tecla le corresponde una nota musical. La última columna indica la frecuencia correspondiente (en Hertz):

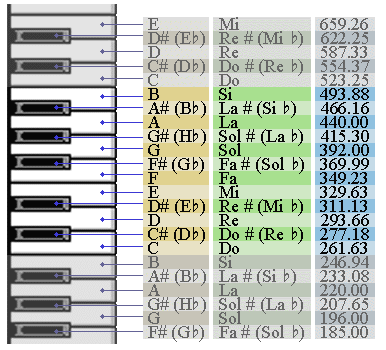
En este esquema se puede ver que las teclas forman grupos de 12 (7 blancas y 5 negras), y estos grupos se repiten de izquierda a derecha. Cada octava tecla blanca cierra un grupo y abre el otro, y por eso la distancia musical entre esas teclas se llama octava (normalmente se llama octava también el mismo grupo de 12 teclas), y su escala es igual a 2:1 - esto es, la frecuencia de la misma nota de siguiente octava es el doble, y la de octava anterior es la mitad. La distancia de dos octavas le corresponde a la relación de frecuencias de 4:1, tres octavas - 8:1 etc.: para sumar distancias tenemos que multiplicar las relaciones de frecuencias. La nota "La" (o "A") es la nota de etalón - su frecuencia es 440 Hz.

Así a partir de un sonido original obtenemos diferentes notas armoniosas. Haciendo un pequeño esquema nos aclararemos mejor: 

Nota	Frecuencia	Long. cuerda
Original	F	L
Octava justa	2f	(1/2)L
Quinta mayor	(3/2)f	(2/3)L
Cuarta justa	(4/3)f	(3/4)L
Tercera mayor	(5/4)f	(4/5)L
Tercera menor	(6/5)f	(5/6)L

si suponemos que la nota inicial es el do, entonces, la octava, quinta y cuarta son las notas: 

Nota base	Cuarta	Quinta	Octava
Do	Fa	Sol	Do (1 octava más alta)

que corresponden a la cuarta, quinta y octava notas respectivamente de la escala diatónica (las teclas blancas del piano), que veremos un poco más adelante.

Esta ordenación de los sonidos musicales ha sido fruto de un largo proceso. Desde la elección de un sonido base, a partir del cual construir el resto, a la determinación del intervalo que hay entre una nota y la siguiente.
Así, una escala es una serie de notas ordenadas de forma ascendente o descendente, donde a la primera de las notas se la llama tónica.

Escala musical occidental (actual)

Se llama escala musical a la sucesión de sonidos constitutivos de un sistema (tonalidad) que se suceden regularmente en sentido ascendente o descendente, y todos ellos con relación a una nota que da nombre a la escala, o tónica.
La sucesión de sonidos en una escala es por movimiento conjunto, y se hace según las leyes de la tonalidad.

El origen de la escala musical
La escala actual (escala occidental) es el resultado de un largo proceso de aprendizaje de las notas. Los pitagóricos construyeron un aparato llamado monocordio que se componía de una tabla, una cuerda tensa y una tabla más pequeña que se iba moviendo por la grande. 

La construcción de la escala musical
La escala diatónica es la formación de una escala a partir de las distancias de tono y semitono. Son las más conocidas y usadas y la mayoría de ellas están formadas por siete notas, pero las hay también de seis u ocho.

Ordenadas las notas así: do, re, mi, fa, sol, la, si, y al añadirle un octavo sonido, de nuevo do, hemos formado una escala diatónica:

I	II	III	IV	V	VI	VII	VIII
do	re	mi	fa	sol	la	si	do

Pero, ¿cómo se pueden encontrar las notas de nuestra escala musical a partir de una nota base (tónica)?. Se puede hacer un proceso repetitivo a partir de esta nota, utilizando las quintas y las octavas:

Lo que queremos hacer es encontrar notas armoniosas con la nota base que se encuentren entre la nota original y su octava.

• Supondremos que la nota original tiene una frecuencia f. Entonces, la octava tendrá frecuencia 2f. Queremos encontrar notas que tengan frecuencia entre f y 2f.
• La primera que tenemos es la quinta, la frecuencia es (3/2)*f. Corresponde a una cuerda de longitud 2/3 la inicial.
• El siguiente paso es encontrar la quinta de la quinta. La frecuencia será (3/2)*(3/2)*f=(9/4)*f. El problema es que esa nota tiene una frecuencia más grande que 2f. Lo que hacemos es encontrar una nota una octava más abajo. Es decir, una nota con frecuencia (9/8)*f.

Si vamos repitiendo el proceso obtenemos las notas siguientes:
- f
- (3/2)*f 
- (9/8)*f. Después de haber descendido una octava.
- (3/2)*(9/8)*f = (27/16)*f 
- (3/2)*(27/16)*f = (81/32)*f. Como la frecuencia es más grande que 2f, descendemos una octava y obtenemos (81/64)*f
- (3/2)*(81/64)*f = (243/128)*f

Hemos obtenido 7 notas, contando la octava, que podemos ordenar de frecuencia más pequeña a más grande de la forma siguiente: 

Nota Base	f
	9/8·f
	81/64 ·f
Quinta	3/2·f
	27/16·f
	243/128·f
Octava	2·f

De esta forma hemos obtenido 6 notas dentro de una octava. Pero si nos fijamos en la razón de frecuencias de una nota y la anterior, parece que hay un agujero entre (81/64)*f y (3/2)*f. Curiosamente entre estos dos valores se encuentra (4/3)*f, que corresponde a lo que hemos llamado cuarta.

(9/8):1=9/8	1,125
(81/64):(9/8)=9/8	1,125
(3/2):(81/64)=32/27	1,185
(27/16):(3/2)=9/8	1,125
(243/128):(27/16)=9/8	1,125
2:(243/128)=256/243	1,053

Añadiendo la cuarta, nos queda una escala de 7 notas con estas razones entre las frecuencias: (en la columna de la derecha hemos puesto el nombre de la nota que correspondería si la nota base fuese el do):

	Frecuencia	Razón nota anterior
Tónica	F		Do
Segunda	9/8·f	9/8=1,125	Re
Tercera	81/64·f	9/8=1,125	Mi
Cuarta	4/3·f	256/243=1,053	Fa
Quinta	3/2·f	9/8=1,125	Sol
Sexta	27/16·f	9/8=1,125	La
Séptima	243/128·f	9/8=1,125	Si
Octava	2f	256/243=1,053	Do

Estas son las 7 notas de la escala diatónica (que se corresponden a las teclas blancas del piano), la octava es la misma que la anterior una octava más alta. De cualquier forma, en una octava se utilizan 12 notas. Las 5 notas restantes se simbolizan añadiendo a la derecha el carácter # (sostenido) o b (bemol).

Podemos ver que hay dos razones diferentes: el tono 9/8 y el semitono 256/243. La pregunta que nos hacemos es qué relación hay entre las dos razones. Se puede ver que dos semitonos hacen casi un tono (256/243)2 =1,109, pero no es exactamente el mismo.

Si ahora utilizásemos las cuartas para ir encontrando nuevas notas armoniosas, comenzarían a salir las "teclas negras" del piano, es decir, los sostenidos y los bemoles. Cuando la escala queda completa con 12 notas (las teclas negras y las blancas), esto es lo que se llama la escala cromática .

El pentagrama

 

En música la representación gráfica de los sonidos se hace por medio de unos símbolos (las notas), que se escriben sobre una pauta llamada pentagrama. El pentagrama es una manera de realizar una notación musical de tal modo que la misma sea fácilmente transmisible a otras personas. Esto significa que así como las letras del alfabeto se juntan para formar una frase, de la misma manera los símbolos musicales se juntan en el pentagrama para formar una canción que puede ser interpretada por un instrumento musical o cantada por la voz del ser humano.

Un típico pentagrama en clave de Sol:

Básicamente los pentagramas están formados por un conjunto de cinco líneas dispuestas de forma paralela. A la izquierda del conjunto de líneas aparece un símbolo distintivo llamado "clave". Esta clave es la que determinará a qué nota musical corresponde cada uno de los símbolos musicales que aparecen en el pentagrama. En el gráfico anterior encontramos un símbolo que identifica a la "clave de Sol": . Existe una variedad considerable de claves en otras notas como Do y Fa , por ejemplo. Como vemos a continuación, el símbolo de laclave de Fa es: 

Un pentagrama en clave de Fa:

La interpretación del pentagrama

Las notas musicales que aparecen dentro del pentagrama pueden colocarse justo encima de alguna de las líneas o en los espacios entre las mismas. Según la clave que corresponda (Sol, Do, Fa, etc.) y la ubicación específica entre las líneas, cada símbolo musical nos brindará información sobre una única nota. La duración en el tiempo de la misma vendrá dada por las características del símbolo musical utilizado.

La nota, gracias a su aspecto y su posición, permite definir simultáneamente tres parámetros:
- La posición vertical de la nota define su altura (aguda o grave). Cuanto más arriba se sitúe la nota sobre las líneas o los espacios del pentagrama, más aguda será.
- La posición horizontal de la nota define cuando es emitida. Así, el eje horizontal del pentagrama define una escala de tiempo creciente desde la izquierda hacia la derecha. Si existiesen dos notas en la misma columna, estarían emitidas simultáneamente.
- La forma de la nota define su duración. Duraciones estándar de notas están definidas en solfeo; cada una es dos veces más corta que la siguiente. Así, se tiene:
La redonda , blanca 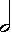, negra 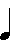, corchea  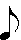, semicorchea  , fusa 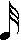, etc.
Así, una blanca es dos veces más corta que una redonda, una negra dos veces más corta que una blanca...

La escala temperada

  

Como un tono no es exactamente dos semitonos, había lugares donde los intervalos eran más grandes o más pequeños que en otros lugares. Esto daba problemas para afinar instrumentos con intervalos fijos como el piano o la guitarra. Es para esto que se creó la escala temperada.

El temperamento es la forma musical de mantener series dentro de un espacio definido. La transición de la afinación pitagórica a la temperada tomó siglos, y ocurrió de una manera paralela al cambio en la relación entre música y matemáticas.
En el siglo XII, compositores e intérpretes el querer separarse de la tradición pitagórica crearon nuevos estilos y tipos de música como el canto monódico gregoriano que poco a poco fue evolucionando en música polifónica con diferentes instrumentos y voces.

La creación de composiciones más complejas llevó a experimentar con afinaciones alternativas y temperamentos; los experimentos de afinación derivaron en un cambio de la afinación pitagórica llamada la afinación justa. Las nuevas afinaciones seguían utilizando las matemáticas para calcular los intervalos, pero no necesariamente seguían los principios pitagóricos. Ahora eran utilizadas de una forma práctica y no como un fin; este cambio de actitud causó desacuerdo entre los matemáticos, quienes querían una adherencia estricta a sus fórmulas, y los músicos que buscaban reglas fáciles de aplicar. De hecho, los músicos empezaron a basarse más en su oído y menos en el monocordio.

En el siglo XVIII, músicos como Juan Sebastián Bach empezar a afinar sus instrumentos usando el temperamento, es decir, una escala en la que los doce sonidos fueran afinados sin diferencia entre un fa sostenido y un sol bemol. La complejidad de las modulaciones lo necesitaba.
Juan Sebastian Bach compuso el clave bien temperado, que consiste en 24 piezas en las doce tonalidades, usando el modo mayor y menor de cada una de ellas, demostrando de esta manera las posibilidades de modulación creadas por una afinación igual.

La cantidad de notas que tiene esta escala es la misma, pero la forma de afinación es diferente. En la escala temperada, la razón entre la frecuencia de una nota y la anterior es siempre constante.

Si llamamos r a esta razón, se cumplirá que las frecuencias formaran una progresión geométrica del tipo:

f, f·r, f· r2, f·r3, f·r4, ..., f·r12 = 2·f

de lo que se deduce que r12 = 2, de donde r = = 1,059...

Esta escala resuelve los problemas de afinación, pero no podemos olvidar que las notas más armoniosas eran las que se había encontrado mediante el método geométrico, es decir las de la escala cromática. Instrumentos sin intervalos fijos como violines, contrabajos, etc. pueden utilizar la afinación de la escala cromática.

La escala natural

 

El oído humano tiene una "construcción" tal, que los sonidos cuyas frecuencias están en la proporción simple (2/1, 3/2, 4/3 etc), suenan juntos de una manera agradable. Por otro lado, casi todos los procesos físicos que producen sonidos, además de la frecuencia principal (o el tono básico) producen también "armónicas", es decir, las frecuencias que son dos, tres, cuatro -una cantidad entera- veces más altas. El conjunto de las armónicas constituye el timbre que es único para cada instrumento musical.

Escogeremos como base la frecuencia de 55 Hertz (esta frecuencia es absolutamente arbitraria, la única razón es que nos lleve a la frecuencia 440 Hertz que es un etalón musical contemporáneo) y vamos a multiplicarla por 2, 3, 4, etc. Obtendremos la siguiente serie:

55; 110, 165; 220, 275, 330, 385; 440, 495, 550, 605, 660, 715, 770, 825; 880

Colocaremos estas frecuencias en sus octavas correspondientes, y arreglaremos la serie en forma de una tabla: 

Octava 1	55
Octava 2	110				165
Octava 3	220		275		330		385
Octava 4	440	495	550	605	660	715	770	825
Octava 5	880
	A	B	C	D	E	F	G	H

Observamos que la segunda octava tiene dos notas, la tercera - cuatro, y la cuarta - ocho, eso es, ¡una octava completa natural! Ahora vamos a calcular las distancias entre las notas: 

440	8:9	495	9:10	550	10:11	605	11:12	660
A4		B4		C5		D5		E5
1:1		9:8		5:4		11:8		3:2

12:13	715	13:14	770	14:15	825	15:16	880
	F5		G5		H5		A5
	13:8		7:4		15:8		2:1

En las celdas superiores intermedias se indica las distancias entre las frecuencias vecinas, y en las celdas inferiores, las distancias con respeto a la frecuencia principal, que en nuestro ejemplo es 440 Hz. La numeración de octavas (4-a o 5-a) corresponde al estándard contemporáneo.
El producto de todas las relaciones intermedias es igual a 2, esto es, a una octava. La serie ordenada de esta manera se conoce como escala. La escala que acabamos de construir se conoce como escala natural.
La distancia musical entre la nota principal y la segunda armónica es 2/1 - una octava. La distancia musical entre la segunda y la tercera armónica en la música se llama quinta, le corresponde la relacion de frecuencias 3/2. En nuestra escala es la distancia entre las notas A4 y E5. La distancia entre la 3-a y 4-a armónica es cuarta -con la relación 4/3-, como entre las notas E5 y A5. Estos son distancias o intervalos fundamentales en la música.

Simetría y recursividad

Un procedimiento básico para obtener cohesión en una pieza de música es la reafirmación de una secuencia de sonidos una y otra vez, de una forma variada, para evitar la monotonía y dar carácter a la composición.

Algunas de las técnicas usadas para dar unidad a una composición, están basadas en el plano geométrico ya que las transformaciones musicales están íntimamente relacionadas con las transformaciones geométricas básicas. Transformaciones geométricas como la rotación, la traslación y la reflexión las encontramos en la mayoría de las melodías populares y el análisis de las obras maestras musicales nos llevará a encontrarlas.

Así, una frase musical tendrá motivos que se repiten en forma idéntica o se repiten en forma más aguda o más grave; en otras ocasiones, en vez de subir, bajan o retroceden. Este es un recurso muy utilizado, aunque normalmente no lo asociamos con las Matemáticas.

Aritmética modular

Una de las cosas más necesarias para que la música "funcione" es que tenga unidad. Es claro que una cantidad de sonidos que se relacionen entre sí sin nada que los relacione (digamos las esquilas de un hato de ovejas, superpuestas al murmullo de un rio, mientras pasa un helicóptero y al lado otro excursionista tiene la radio demasiado alta), va a ser difícil de percibir como experiencia musical unitaria, aunque puede admitirse que haya quien disfrute de tal experiencia sonora.

Necesitamos más bien algo que nos haga pensar que la obra se relaciona consigo misma, que cada momento que oímos, se relaciona con los que hemos oído o los que nos quedan por oír —las formas en que se puede conseguir esto son incontables, y no excluyen el contraste—.

Dentro de las formas más primitivas —que está lejos de significar toscas— de conseguir esto, tenemos la repetición de una línea melódica no demasiado larga. Esta repetición aportará unidad a la obra, logrando que nuestro oído alcance satisfacción. Esta práctica es el origen, por ejemplo, de todas las formas musicales basadas en el ostinato.

Lo malo de este procedimiento es que puede, fácilmente, producir demasiada unidad, y acabar resultando aburrido.

Otra de las posibilidades para crear unidad es limitar el rango de frecuencias con que trabajamos: en lugar de emplear todo el espectro de frecuencias comprendido entre los 40 y los 20.000 Htz que abarca el oído humano, limitamos estas frecuencias a unas pocas. Así, elegimos unas pocas frecuencias con las que trabajar, y formamos escalas.

El intervalo de octava, por motivos en parte físicos (es singularmente presente en la naturaleza) y en parte biológicos (el registro de mujeres y hombres cuando cantan juntos difiere normalmente en esa cantidad), acaba dominando la elección de esas frecuencias, de forma que lo usual en todas las culturas es que dentro de una octava se elijan ciertas frecuencias y se repitan en todas las demás. Los pocos casos en que eso no ha sido exacto es cuando se ha dispuesto de instrumentos —las steel drums tropicales, por ejemplo—, cuyo rendimiento difiere en cada octava.

Con esto se llega a que las escalas se han tratado de una forma que, a partir de ahora, denominaremos modular. Si observamos un reloj, no nos parece ilógico que después de las doce venga la una. O a quien juegue a las cartas, tampoco le parecerá extraño que en la baraja francesa después de la reina y el rey vengan el as y el dos. Son casos, por así decirlo, en que imponemos un orden pero no un principio y un fin.

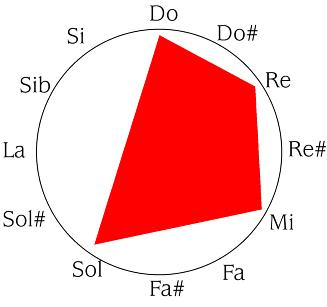
Observemos una escala diatónica normal.

       

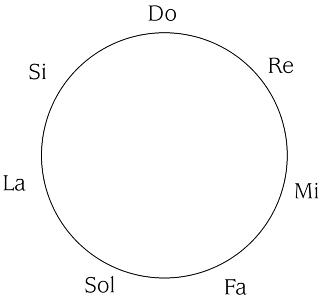
Podemos observar que se ha optado por representarla en círculo. A todos nos han hecho en el colegio aprender "do, re mi, fa, sol, la, si, DO". Por tanto es sensato adoptar una disposición circular que represente esta modularidad.

Aquí podemos observar lo mismo con una escala cromática.

                

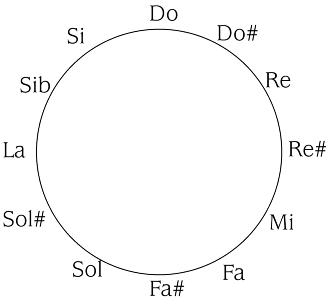
Volvamos ahora a cómo usar repeticiones y aportar además de unidad, variedad. Para nuestro ejemplo, digamos que el fragmento melódico que deseamos repetir es DO- RE- MI- SOL, que represento a continuación como una figura geométrica dentro de la escala diatónica.

                 

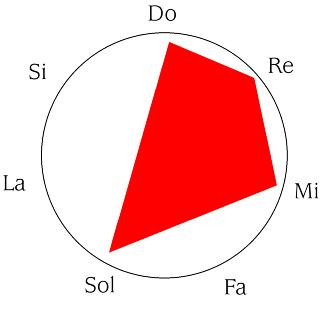
Una primera posibilidad consistiría en lo que llamamos transportar, que consistiría en repetir las mismas distancias desde una nota diferente, si comenzamos desde RE, que es la siguiente a DO, tenemos que:

• La siguiente a RE, es MI
• La siguiente a MI, es FA
• La siguiente a SOL, es LA

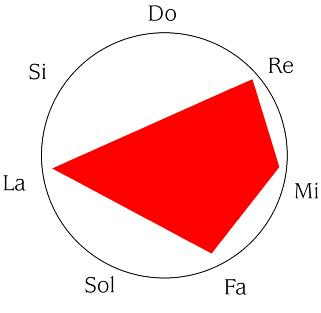
De forma que nuestro D0-RE-MI-SOL, se transforma en RE- MI- FA- LA. El oído se sorprende ante lo nuevo, reconoce el parentesco y queda satisfecho, lo que es una suerte porque es un procedimiento de construcción melódica que ha marcado la inmensa mayoría de la música, de, por ejemplo, Bach —un caso diáfano es la invención número 1— o Mozart.

Es una operación equivalente a un giro, si seguimos con nuestra analogía visual.

                  

Otra forma en que podríamos haber hecho esto es numerando las notas:

• Do=0
• Re=1
• Mi=2
• Fa=3
• Sol=4
• La=5
• Si=6

Con lo que nuestro DO- RE- MI- SOL, se convierte en [0, 1, 2, 4].

Puesto que la diferencia entre 0 y 1 (do y re, a donde queremos transportar el fragmento) es uno, no tenemos más que añadir 1 a cada miembro de esta hilera de números para conseguir [1, 2, 3, 5], que al retraducir, nos da RE- MI- SOL- LA. Los músicos quizá puedan pensar que es más difícil hacerlo así, pero es un procedimiento que conviene conocer.

Es obvio que para un transporte ascendente debemos sumar, y para uno desdendente, restar.

Hay sin embargo, un problema con este procedimiento. Supongamos que quiero transportar el fragmento a FA. La diferencia entre DO y FA es 3, con lo que [0, 1, 2, 4], se convertiría en [3, 4, 5, 7]. Y resulta que 7 no lo tenemos definido en la tabla anterior.

La solución es restar 7 (el número de notas de esta escala) de todo número mayor o igual que 7, tantas veces como sea necesario hasta obtener un número entre 0 y 6. De la misma forma, si en algún momento obtuviésemos resultados negativos, habría que sumar 7, hasta conseguir lo mismo.

En otras escalas de un número diferente de notas, los resultados serían distintos en el transporte. En la escala cromática, DO- RE- MI- SOL se convertiría en RE- MI- FA#- LA. En los grafismos,

                  

se convertiría en

                    

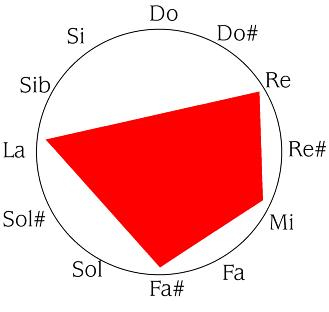
Y, obviamente, en el procedimiento numérico, hay que numerar de 0 a 11, y restar o sumar doces en consecuencia.

Técnicas de transformación

Una de las ventajas que nos proporcionaba el transporte era la de provocar simultáneamente unidad y variedad. Es evidente que cualquier técnica de este tipo nos va a resultar extraordinariamente útil, por su economía.

La primera técnica se denomina inversión o movimiento contrario. Consiste en respetar el perfil melódico, pero invertir la dirección del intervalo. Es decir: los saltos melódicos ascendentes los convertimos en descendentes y viceversa.

El ejemplo que veníamos usando era DO- RE- MI- SOL. DO- RE y RE- MI son segundas ascendentes, así contestaremos con segundas descendentes, DO-SI y SI-LA. MI- SOL es una tercera ascendente, así que contestaremos con una tercera descendente desde LA, LA- FA, así que la inversión será DO- SI- LA- FA

Dentro de nuestra analogía gráfica, significa que

                 

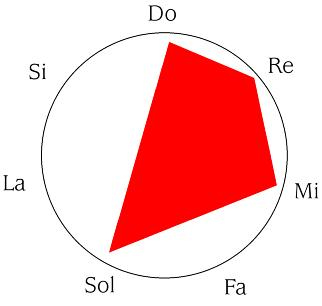
se convierte en

                  

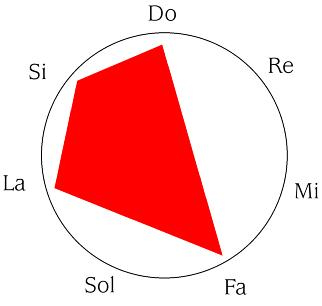
que, como podemos observar, es claramente la figura simétrica al original.

Numéricamente, expresábamos DO- RE- MI- SOL como [0, 1, 2, 4]. ¿Podemos a partir de estas cifras calcular la inversión?

Sí. Vamos a restar cada uno de estos elementos de 7, que es el número de notas de la escala que hemos elegido emplear.

• 7-0=7
• 7-1=6
• 7-2=5
• 7-4=3

Con lo que nos queda [7, 6, 5, 3].

Volvemos a encontrarnos con que 7 no está definido. Y la solución es la misma que para el transporte: restamos 7 (o el número de notas que tenga la escala) tantas veces como sea necesario hasta encontrarnos con un número entre 0 y 6 (o entre 0 y el número de notas de la escala). Con lo que nos queda [0, 6, 5, 4], o sea, DO- SI- LA- FA.

Lógicamente, podemos combinar la inversión y el transporte, de forma que obtenemos una buena cantidad de versiones del material original, que cumplen simultáneamente el objetivo de proporcionar unidad y variedad.

Hay también que decir que estos procedimientos se aplican empleando el sentido común. Hay materiales que funcionan especialmente bien o especialmente mal al someterlos a la inversión a a cualquier otra de las transformaciones. No hay ni que decir que el compositor empleará los que funcionen bien.

El siguiente procedimiento se denomina retrogradación. Hasta ahora, nos ha sido cómodo ignorar que las notas que hemos elegido tienen un determinado orden. Ahora necesitamos tenerlo en cuenta. En forma de notas, no hay problema: DO- RE- MI- SOL en su orden normal de lectura aporta toda la información.

En forma gráfica, podemos indicar el orden empleando una flecha.

                   

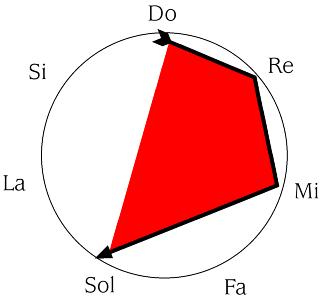
Y en forma numérica, sigue valiendo el orden normal de lectura.

Pues bien, la retrogradación va a consistir en comenzar desde la última nota hasta alcanzar la primera, o, sí se prefiere, en leer de derecha a izquierda las notas.

DO-RE- MI- SOL se convierte en SOL- MI- RE DO.

                     

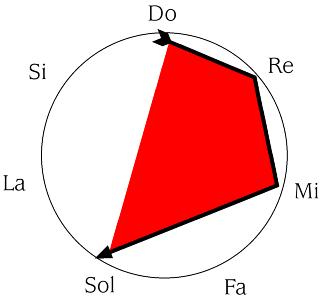
se convierte en

                     

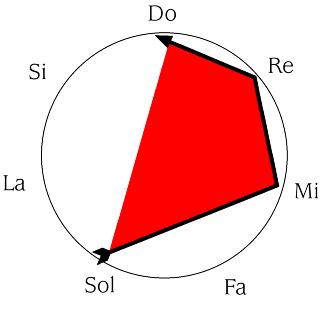
Y [0, 1, 2, 4] se convierte en [4, 2, 1, 0]

La última técnica de transformación temática se denomina inversión retrógrada, y consiste en la aplicación de la inversión y la retrogradación simultáneamente. El orden en que se apliquen es irrelevante, puesto que nos saldrá la misma estructura interválica, aunque transportada, según empecemos por una u otra.

DO- RE- MI- SOL se convierte en FA- LA-SI-DO

En forma gráfica, aplicamos la simetría y cambiamos el orden de lectura.

                  

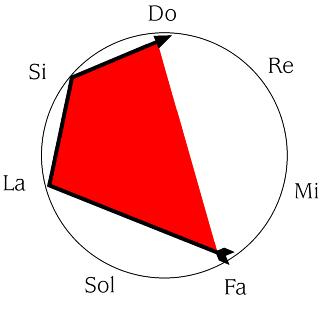
Y, numéricamente, [0, 1, 2, 4], se convierte en [4, 6, 7, 0].

Disponemos entonces, para un material melódico dado, de cuatro versiones:

1. La forma original, que representamos por O.
2. La forma invertida, que representamos con una I.
3. La forma retrograda, que representamos con una R.
4. La forma sometida a inversión retrógrada, que representamos con IR.

Cada una de estas cuatro versiones puede ser sometida a transporte, de forma que disponemos de 28 (7*4, número de notas de la escala multiplicado por el número de versiones) posibilidades de uso. Más, de hecho, si podemos cambiar la escala de referencia.

Ejemplos de aritmética modular

La Fuga es un procedimiento de construcción musical o forma musical que se podría definir como una composición polifónica basada en el contrapunto entre varias voces. Su principal característica se basa en su estructura ya que las voces o partes del arreglo reproducen sucesivamente el mismo tema en imitación de las otras en diferentes tonalidades.

Johann Sebastian Bach es el más destacado; llevó la fuga a su apogeo en su obra El arte de la fuga (1749-1750). Durante los siguientes siglos se "redescubrió" la fuga; casos famosos son la Gran Fuga para cuarteto, opus 133 (1825) de Beethoven, y los 24 preludios y fugas opus 87 de Shostakovich.

Johann Sebastian Bach (1685-1750)

El arte de la fuga 2

El arte de la fuga 6

El compositor polaco Chopin describió la fuga como “lógica pura”. Era un gran admirador de la obra de Bach y siguiendo sus pasos, aplicó el principio del contraste, alternando los modos mayor y menor, en su obra 24 preludios.

Frederic Chopin (1810-1849)

Aunque teóricamente daría igual qué tonalidad se eligiese (los 12 semitonos son iguales), puede que el pianista, inconscientemente, no toque todos con el mismo ánimo pues la distribución de teclas negras y blancas varía en cada caso.

Las tonalidades de estos preludios de Chopin siguen el orden: Do mayor, La menor, Sol mayor, Mi menor, Re mayor, etc. ¿Qué orden es este?

Podemos disponer estas 24 tonalidades en un reloj. La parte externa indica el modo mayor y la interna el modo menor. Así expuesto, se ve claramente que Chopin sigue “el ciclo de quintas”. Es decir, cada nueva tonalidad está 7 semitonos más arriba que la tonalidad anterior del mismo modo. Matemáticamente, esto equivale a sumar 7 en sentido horario.

 

Repetición y simetrías

La repetición es, probablemente, el procedimiento más usado en música, de hecho, la repetición constante puede causar un efecto hipnótico. También puede provocar una adaptación del oído, como cuando dejamos de percibir el sonido de una lámpara fluorescente.

La repetición no continúa indefinidamente en su manifestación física,  pero nos ofrece una imagen del infinito que en potencia contiene.

Las oberturas de Rossini son un ejemplo de traslación melódica, en dichas obras las frases se repiten, cada vez con más intensidad (crescendo), provocando la expectativa de continuación. El climax se alcanza rompiendo la traslación.

Gioachino Antonio Rossini (1792-1868)

Rossini compuso algunas de las obras más conocidas de todo el repertorio operístico. Una curiosidad de su obra es que recorre las principales ciudades italianas presentando sus óperas, pero en esta época se producen muchos de sus conocidos "pasticcios", o autoplagios que se producían porque tenía que componer numerosas obras cada año y, no estando las ciudades italianas especialmente bien comunicadas, se dedicaba a cortar y pegar trozos completos de óperas anteriores para presentarlas en el siguiente lugar de estreno.

La simetría en música es, sin duda, un caso muy especial. El propio concepto de ritmo a menudo va ligado a la repetición de un determinado sonido o composición, pero donde podemos descubrir curiosas simetrías es en el análisis de las vibraciones emitidas por los diferentes instrumentos. Unas simetrías en el propio pentagrama en el que se ha creado una composición pueden conducir a curiosos efectos auditivos.

Existen interesantes ejemplos en la música clásica: Bach ("Preludio"), Scarlatti ("Sonata en G mayor"), Schumann ("Lotosblume"), Wagner ("Die Meiestersinger")... En la mayoría de estos casos encontramos distribuciones de las notas generadas por traslación o simetría bilateral o giros de media vuelta.

¿Qué pasaría si invirtiéramos toda una partitura?. En general resultaría una composición absurda. Pero hay casos en los que la nueva melodía invertida sí que se puede interpretar. Un bello ejemplo es el "Scherzo-Duetto" de Mozart para dos violines: la obra la pueden interpretar a la vez dos violinistas, cada uno de los cuales lee la partitura en un sentido diferente.

A continuación podemos apreciar dos claros ejemplos de obras maestras que se basan en la repeticióny en la simetría:

El bolero de Ravel

Quinta sinfonía de Beethoven

El sonido en términos matemáticos

En este trabajo se trata la relación entre las Matemáticas y la Música desde una vista totalmente teórica matemática. Se analiza las contribuciones que sobre el sonido han realizado muchos grandes matemáticos a lo largo de la historia y en especial en los siglos XVII, XVIII y XIX.

Se centra fundamentalmente en el problema de las cuerdas vibrantes y en la discusión que tal problema suscitó entre los matemáticos de cada época. Desde Brook Taylor a principios del XVIII hasta la resolución final del problema por parte de Joseph Fourier ya bien avanzado el siglo XIX, cuando se produjo un interesante debate en el que participaron entre otros, Johann Bernoulli y especialmente su hijo, Daniel, Leonhard Euler, Jean-le-Rond D’Alembert, J. L. Lagrange y L. Dirichlet.

El índice del trabajo se resume en:

1 Introducción

2 Preliminares: El sonido
3 La vibración fundamental de B. Taylor
4 Vibración de las cuerdas sonoras
5 El método de D’Alembert. Reflexión de ondas
6 El método de Fourier. Las Leyes de Mersenne
7 Timbre
8 Vibración en los tubos sonoros
9 Vibraciones de varillas, placas y membranas2 Preliminares: El sonido 

10 La propagación del sonido 

De la notación musical a la notación matemática

Introducción histórica, la teoría de conjuntos en música

Después de Brahms, la tonalidad en la música occidental empezó a descomponerse. Mientras que antes los compositores se basaban en un tono y área específica alrededor del cual organizar las notas (por ejemplo, un concierto en Do Sostenido Menor), la idea de una estructura tonal de base había quedado trasnochada entrando en el siglo XX.

Los compositores necesitaron un nuevo sistema para organizar sus tonos. Arnold Schoenberg  encabezó el movimiento empezando a escribir música atonal en 1908. Hacia 1923 había desarrollado completamente un sistema de "12 tonos" bajo el cual el compositor organiza las 12 notas en una fila ordenada que somete a diversas manipulaciones para generar el contenido tonal de la composición. Este sistema es conocido como 'serialismo'. 

La Teoría Musical de Conjuntos no es lo mismo que el serialismo, pero ambas comparten muchos métodos e ideas. La Teoría de Conjuntos contempla la definición de conjuntos de notas y organiza la música alrededor de estos conjuntos y sus distintas manipulaciones. El análisis de las clases de estos conjuntos es el resultado de los esfuerzos de los teóricos de la música por revelar los sistemas que compositores como Schoenberg y sus seguidores usaron para organizar el contenido tonal en sus trabajos. Ten presente que los conjuntos y sus clases determinan únicamente el contenido tonal; los compositores continúan libres de modificar cualquier otro aspecto musical de acuerdo con sus deseos artísticos. 

En su día, Mozart, Haydn, y Beethoven fueron englobados colectivamente como "La Escuela Vienesa" de los compositores. Las ideas de Schoenberg sobre la música fueron tan poco ortodoxas y cambiaron tan radicalmente la faz de la historia de la música, que junto con dos de sus discípulos en Viena, Alban Berg y Anton Webern, son conocidos como "La Segunda Escuela Vienesa". 

Ejemplo práctico

La primera idea que surge es tomar una melodía, asignar una notación matemática para ella y de este modo llevarla al lenguaje de conjuntos y observar diferentes comportamientos y propiedades que pueda tener determinada obra, o tal vez, qué operaciones se pueden realizar con éste conjunto para formar un nuevo conjunto que me ofrezca una nueva melodía.

Los elementos que inicialmente tendremos en cuenta serán: el orden dentro de la partitura, la altura específica y la duración de cada nota musical, para lo cual organizaremos ternas ordenadas (a,b,c) que representan los elementos anteriormente mencionados respectivamente.

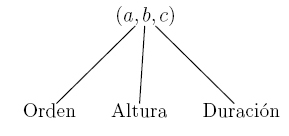
Construcción de los conjuntos

A continuación se va a proceder a construir los tres conjuntos que acabamos de definir en la terna, para ello se definen los siguientes conjuntos:

• Conjunto O que determinará el orden
• Conjunto A que determinará la altura
• Conjunto D que determinará la duración

Primeramente, el conjunto O vendrá dado por el número de elementos de que conste la terna, así:

Para construir el conjunto A, que determina la altura de la terna ordenada, se consideran las alturas específicas que roduce un piano, así DO1 es la nota más grave y DO8 la más aguda como muestra la siguiente tabla:

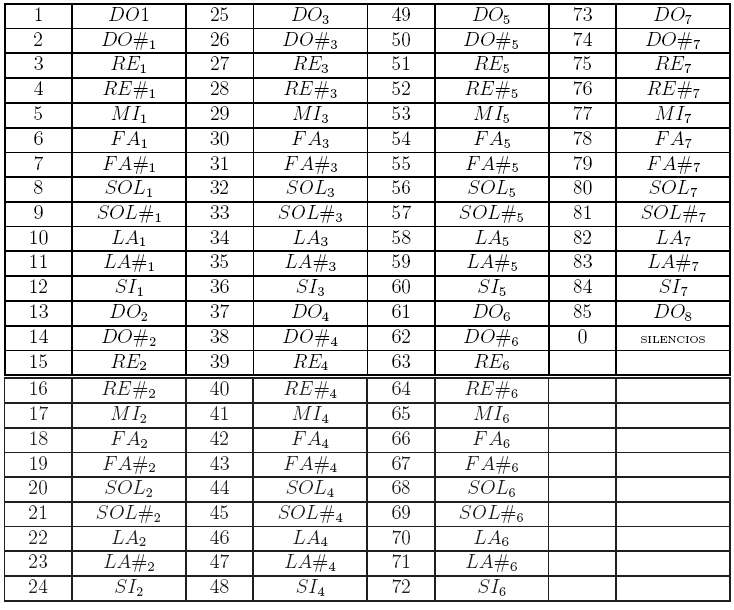
De este modo, le asignamos a cada altura específica un número natural como muestra la tabla anterior, luego tenemos que:

Del mismo modo, para el conjunto D que define la duración de la terna, se asigna a cada figura musical un número natural de este modo:

Así tenemos:

Luego podemos decir:

El conjunto M

Con esto es posible formar un gran conjunto, que sería el conjunto referencial, con todas las posibles combinaciones de ternas ordenadas. Se podría empezar con un referencial que involucre una cantidad no mayor de 500 notas, y así se obtendría un conjunto de 467.500 ternas para trabajar. Este conjunto se denomina conjunto referencial musical (M) para una cantidad n de notas.

Sean O, A y D los conjuntos determinados por la asignación de orden, alturay duración de una obra musical respectivamente, donde:

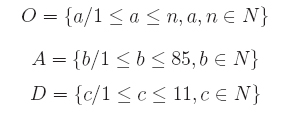
El conjunto M se define como:

M = O x A x D

Ejemplo

Tomaremos un fragmento de un compás de una melodía determinada, para describir cómo le asignamos una notación matemática. Tenemos por ejemplo el siguiente fragmento:

En la figura tenemos la parte inicial (primer compás) de una partitura, en este caso en 4/4 y con su armadura que nota la tonalidad de la melodía (ya se vió en apartados anteriores el sistema temperado), en este caso será Do mayor.

Se puede apreciar que existen dos notas diferentes, Mi y Re, cada una con una duración de corchea que serán dos ternas diferentes que vendrán definidas por (1,29,9) y (2,27,9). De este modo podemos establecer ternas diferentes para cada nota que se ha de interpretar en determinada obra musical.

De lo anterior se obtiene que para cada altura es posible asignar 11 duraciones diferentes, lo que da como resultado 935 combinaciones diferentes; ahora bien, la primera coordenada indica el orden de cada nota, lo cual nos permite conocer la cantidad de notas que se interpretan en alguna obra; teniendo en cuenta esto último podemos encontrar melodías a una sola voz de 250, 300 o más notas.

Algunas funciones frecuentes en la composición musical

Ya se han visto en un apartado anterior las técnicas de transformación más frecuentes a la hora de interpretar y de componer una obra musical; ahora se van a volver a ver algunas de ellas pero como funciones aplicadas a los conjuntos que se acaban de describir.

Función de transportar

Transportar hace referencia a la alteración de las frecuencias en un rango determinado, así la función de transportar que afecta a cada nota se producirá de modo tal que dicha nota tomará valores a una distanica no mayor de 11 unidades, así por ejemplo RE7 no puede convertirse en un RE6 o en RE8; así se define la función de transportar (T):

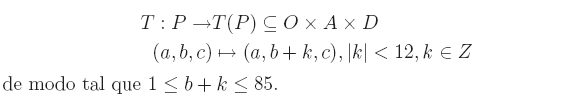
A continuación se ve un ejemplo gráfico de como afectaría esta función en un segmento de una obra:

Función de octavar

Cuando se habla de octavar una nota, se está haciendo referencia al hecho de duplicar la frecuencia de ésta, así la nota que se producirá es la misma pero con una mayor agudeza; por ejemplo la octava superior de MI4 es MI5 y la octava inferior es MI3. Así octavar una nota será sumar o restar 12 unidades a ésta, luego se define la función octavar (O) así:

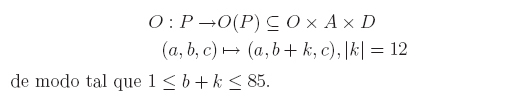
A continuación se ve un ejemplo gráfico de como afectaría esta función en un segmento de una obra:

 

Función de inversión

La inversión es el cambio de posición de las ternas de P, es decir, que para un conjunto P de orden n se realiza la siguiente operación, la terna (1,b1,c1) pasará a tomar la posición n, la terna (2,b2,c2) tomará la posición n-1, la terna (3,b3,c3) tomará la posición n-2 y así sucesivamente hasta la terna (n,an,bn) que tomará la posición 1. Así, se define la función de inversión (I):

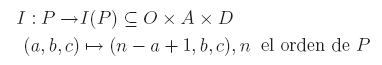
Conclusión

Con las funciones anteriormente mencionadas se pueden transformar melodías en otras nuevas y tener una herramienta para la composición de piezas musicales después de un proceso de selección adecuado de ternas ordenadas.

PROPOSICIÓN: La composición de las funciones T, O e I definidas sobre un conjunto P (conjunto definido a partir de la notación musical) es conmutativo. Es decir, sea t una terna ordenada de P, entonces:

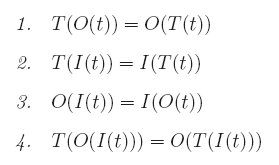
Ejemplos históricos de las Matemáticas en la Música

Es prácticamente desconocida la aplicación de algunos conceptos matemáticos a otros aspectos de la Música como son el análisis, los aspectos estéticos, la composición y la Teoría Matemática de la Música. A continuación veamos cómo algunos matemáticos y músicos han aplicado conceptos matemáticos en la Música a lo largo de la historia.

Mozart

Wolfgang Amadeus Mozart nació en (Salzburgo, actual Austria; 27 de enero de 1756 - Viena; 5 de diciembre de 1791), es considerado como uno de los más grandes compositores de música clásica del mundo occidental. A pesar de que murió muy joven (apenas a los 35 años), nos ha legado una obra tan importante que abarca todos los géneros musicales de su época. Según el testimonio de sus contemporáneos era, tanto al piano como al violín y la viola, un virtuoso.

Mozart, en 1777, a los escasos 21 años de edad, escribió un "Juego de Dados Musical para escribir valses con la ayuda de dos dados sin ser músico ni saber nada de composición". Escribió 176 compases adecuadamente y los puso en dos tablas de 88 elementos cada una:

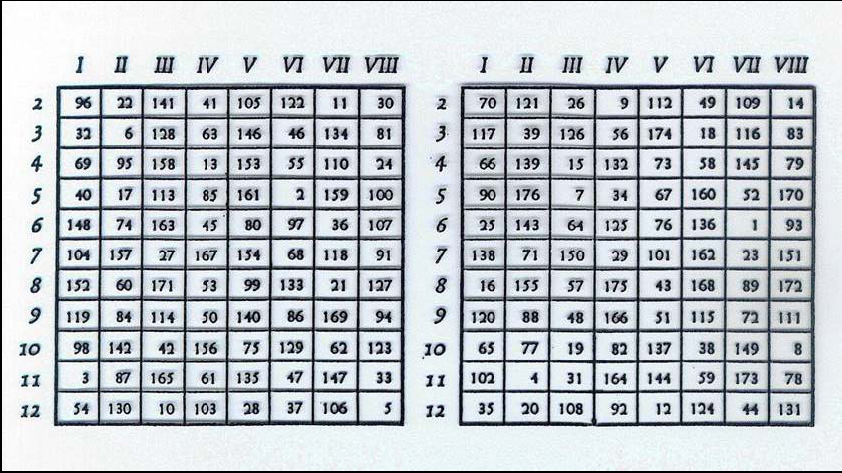
El juego comienza lanzando los dos dados, de tal manera que tenemos 11 números posibles (del 2 al 12) y hacemos 8 tiradas obteniendo distintos compases excepto los de la última columna que son iguales (éstos últimos con dos posibilidades: una para la repetición y otra para continuar con la segunda tabla. La segunda tabla es igual a la primera excepto que tiene otros 88 compases con los de la última columna idénticos.

Así, mediante un simple cálculo, utilizando conceptos del Álgebra Superior, se tienen 1114 valses diferentes, es decir, aproximadamente 3.797498335832 (10e14) valses diferentes. Si se toca cada vals, con repetición de la primera parte, en 30 segundos, se requerirían de 30(11e14) segundos, es decir, 131,857,581,105 días aproximadamente, o bien, 361,253,646 años aproximadamente en tocarlos todos uno tras de otro ininterrumpidamente. Es decir, un estreno mundial de una obra de Mozart cada 30 segundos a lo largo de ¡361 millones de años! (Recuérdese que la antigua edad de piedra comenzó hace unos 35,000 años).

Juego de los dados

Mozart era un aficionado a la matemática y su enorme talento se mostró una vez más. Con este juego tan sencillo ¡dejó la imposibilidad de que intérprete alguno pudiera tocar su obra completa o de que alguna compañía de discos la grabara!

Aún más, nos muestra qué poca idea tenemos de los números grandes como 30(11e14). Existieron y existen compositores que creen que ya todo está agotado con la armonía tradicional, y que por lo tanto hay que buscar un nuevo estilo de música. (Mozart, para este juego, solamente utilizó 176 compases). Aún en estos días, con computadoras y Combinatoria no se podría manejar una pequeña porción de motives musicales puesto que la cantidad de clases de isomorfismo es exorbitante. Por ejemplo, la formula de Fripertinger da un número de órbitas afines de 72 elementos motívicos, que es del orden de 10e36. El número de estrellas en una galaxia está estimado en 10e11. Así, el universo musical es un serio competidor contra el universo físico. También, el uso de métodos estadísticos es requerido para atender la enorme variedad de casos. Ni siquiera las computadoras de la próxima generación podrían manejar todos los casos.

“Yáechik había dicho una vez que llegaría un día, dentro de tal vez miles de años, en el que los seres humanos hablarán con música, y Yárchik lo repite siempre con la misma seguridad. Dice que la música contiene mucha más información que las simples notas. Y que no es una cuestión de simples sentimientos, sino de matemáticas. Que sólo hace falta que el cerebro desarrolle la capacidad de producir y leer esa información. Que algunos, como Mozart, podían hacerlo, y que en su música siguen vivos los mensajes, esperando las mentes que lleguen a ser capaces de leerlos” (Gonzalo Moure, “El síndrome de Mozart”, Edciones SM, 2003,pág.57).

La marcha turca

George Birkhoff

George David Birkhoff (1884-1944) fue el más importante matemático estadounidense del siglo XX.

En 1924 George David Birkhoff (quien trabajó brillantemente en el Problema de los tres cuerpos, Ecuaciones Diferenciales, Teoría General de Relatividad entre otras áreas, miembro honorario de la Sociedad Matemática Mexicana y contribuyente al desarrollo cultural de México) retoma unas ideas que había tenido años atrás pero que no desarrolló por dedicarse exclusivamente a estudios puramente matemáticos.

Pensó que la melodía dependía del orden de las notas escuchadas por el oído. Le pareció que podrían establecerse unas relaciones de orden, guardadas por las notas, y así poder escoger las mejores melodías.

Para él, el problema fundamental de la Estética era el de determinar, para una clase de objetos, las características específicas de las cuales depende el valor estético. Birkhoff considera que hay tres fases consecutivas para la experiencia estética: primero, un esfuerzo preliminar de atención, el cual es necesario para percibir el objeto y que es proporcional a la complejidad C del objeto; segundo, una sensación placentera o medida estética M la cual recompensa este esfuerzo preliminar; y tercero, una certificación de que el objeto posee una armonía, simetría u orden O el cual parece una condición necesaria, si no es que suficiente, para la experiencia estética.

Así, Birkhoff propone la fórmula M=O/C mediante la cual expresa la medida estética como el efecto de la densidad de las relaciones de orden comparadas con la complejidad.
El mismo inquiere lo atrevido de esta fórmula y proporciona algunas justificaciones históricas.

La Estética trata del placer estético y con los objetos que lo producen. Así es que tenemos clases de objetos los cuales pueden ser comparados con respecto a su valor estético (los de clases diferentes no pueden ser comparados). Luego, el problema fundamental de la Estética Analítica es el de determinar los factores estéticos y su importancia relativa.

Percibir un objeto estético requiere de ciertos ajustes y la sensación de esfuerzo o tensión que acompaña siempre a la percepción aparece como la suma de las tensiones a los diversos ajustes automáticos. Así, si A, B, C,... representan estos ajustes, cada uno con tensiones a,b,c,... y si éstas se realizan r,s,t,... veces podemos considerar la suma C=ra+sb+tc+... como la complejidad.

Por otro lado, el orden O corresponde a ciertas asociaciones que intervienen en el acto de percepción. Por ejemplo, la simetría sería una asociación. Si L,M,N,... son asociaciones de varios tipos, cada una con índices de sensación l,m,n,... las cuales ocurren u,v,w,... veces, entonces podemos considerar el total de sensaciones (positivo o negativo O=ul+vm+wn+... como el orden del objeto. Así, la estimación intuitiva de la cantidad de orden O inherente al objeto estético, comparado con su complejidad C, nos proporciona su medida estética.

Obviamente esta teoría matemática solo puede aplicarse a objetos cuyos factores estéticos sean esencialmente matemáticos o formales. Hay otros factores que están más allá de esta teoría, como por ejemplo, las asociaciones acerca del significado de un poema hermoso.

También aplica su fórmula a los acordes diatónicos, armonía y melodía así como a la calidad musical en la poesía. En el caso musical, su teoría está basada en las relaciones de orden entre las notas y puesto que la apreciación de tales relaciones continuamente cambia y se desarrolla, no trata de formar una teoría definitiva de la medida estética que sea válida para el futuro o el pasado. Más bien, considera que el problema principal de la forma musical es el de que dado un conjunto de recursos musicales debemos determinar hasta qué grado las relaciones de orden entre las notas de una composición constituyen una base eficiente de
disfrute musical.

Leibniz

Gottfried Wilhelm von Leibniz (1 de julio, 1646 - 14 de noviembre, 1716) fue un filósofo, matemático, jurista y político alemán, de origen sorbio, nacido en Leipzig en julio de 1646.

Educado en leyes y filosofía, Leibniz jugó un importante papel en la política y diplomacia europea de su época. Ocupa un lugar igualmente grande en la historia de la Filosofía y en la de las Matemáticas. Descubrió el cálculo infinitesimal, independientemente de Newton, y su notación es la que se halla desde entonces en uso general. También inventó el sistema binario, en que se basan casi todas las arquitecturas de computación actuales.

Durante el siglo XVII y principios del XVIII prevalecieron los conceptos de "ingenio" y "buen gusto". En éste último está implícito un esfuerzo de atención, luego un juicio estético intuitivo dependiendo del buen gusto y finalmente el análisis.

Leibniz pudo admitir las percepciones y juicios estéticos como parte del saber y definió la Música como el contar sin saber que se está contando. Esto último concuerda con el concepto de Birkhoff en el sentido de que la densidad de ciertas relaciones ordenadas entre las notas consideradas intuitivamente, miden el efecto estético.

De Crousaz, Rameau y D'Alembert

De Crousaz escribe, que el buen gusto nos hace apreciar, al principio, por sensaciones, aquello que la razón hubiera aprobado.
Rameau observó que una nota musical está compuesta por un sonido fundamental y varias parciales, y que las notas que difieren por una octava son similares en cuanto a su efecto estético y pueden considerarse casi idénticas. Estos hechos conducen al entendimiento de la música occidental.

Fue d'Alembert quien dio una clara presentación del trabajo de Rameau (el cual es cualitativo, a diferencia del tratamiento cuantitativo de Birkhoff). Así, el grado de armonicidad es distinto del agrado o medida estética. Por ejemplo, el unísono y la octava son los más armoniosos de los intervalos pero no los más agradables

Euler

Leonhard Euler nació el 15 de abril de 1707 en Basilea, Suiza. Murió el 18 de septiembre de 1783 en San Petersburgo, Rusia. Vivió en Rusia la mayor parte de su vida. Probablemente fue uno de los más grandes matemáticos de la historia, comparable a Gauss, Newton o Arquímedes.

Perdió la vista de un ojo durante un experimento en óptica, y en 1766 la vista del otro, ya de mayor. Pasó los últimos años de su vida ciego, pero siguió trabajando. Se le considera el ser humano con mayor número de trabajos y artículos en cualquier campo del saber, solo equiparable a Gauss.

Posiblemente es el matemático más prolífico de la historia. Muchos trabajos se los dictó a su hijo mayor cuando ya estaba ciego. A pesar de que su actividad de publicación era incesante (un promedio de 800 páginas de artículos al año en su época de mayor producción, entre 1727 y 1783), la mayor parte de su obra completa está sin publicar.

Euler, en 1739, desarrolló una teoría de consonancia basada en la ley pitagórica. Entre más pequeños sean los números que expresan la relación de vibración de dos notas, éstas serán más consonantes.

De ésta forma, Euler estableció un criterio de armonicidad de cualquier intervalo o acorde que concuerda con los hechos observados. Es interesante que Euler formulara una ley cuantitativa para la medida de la armonicidad.

Así, el concepto general de Euler acerca de la naturaleza del goce estético concuerda completamente con el de Birkhoff, que en palabras de Helmholtz años después, establecían que entre más fácilmente percibamos el orden que caracteriza a los objetos contemplados, estos parecerán más simples y perfectos, y más fácil y gozosamente los reconoceremos. Un orden que cuesta trabajo descubrir, aunque ciertamente nos halague, asociará cierto grado de desgaste y tristeza.

Fibonacci

Leonardo de Pisa o Leonardo Pisano o Leonardo Bigollo (c. 1170 - 1250), también llamado Fibonacci, fue un matemático italiano, famoso por la invención de la sucesión de Fibonacci, surgida como consecuencia del estudio del crecimiento de las poblaciones de conejos, y por su papel en la popularización del sistema de numeración posicional en base 10 (o decimal) en Europa.

Consciente de la superioridad de los numerales árabes, Fibonacci viajó a través de los países del Mediterráneo para estudiar con los matemáticos árabes más destacados de ese tiempo, regresando cerca de 1200.

En 1202, a los 32 años de edad, publicó lo que había aprendido en el Liber Abaci (libro del ábaco o libro de los cálculos). Sobrevive la segunda edición del año 1228. Contenía casi todo el conocimiento aritmético y algebraico de esa época y jugó un papel fundamental en el desarrollo de la matemática occidental, pues a través de él, los europeos se familiarizaron con el sistema numérico indo arábigo.
Contenía muchísimos ejemplos. Veamos uno de ellos, reformulado de la siguiente manera: suponga que los conejos no se reproducen durante su primer mes de vida, pero que a partir del segundo mes cada pareja de conejos produce un nuevo par. Suponga que ningún conejo muere. Si comenzamos con un par de conejos, ¿cuántas parejas de conejos hay a los doce meses y en general a los n meses? La sucesión de las parejas adultas es de la forma:

1,1,2,3,5,8,13,21,34,55,89,144,233,377,...

es decir, la sucesión dada por la fórmula u1=u2=1 y un=un-1+un-2 para n mayor o igual que 2. Esta sucesión se llama sucesión de Fibonacci y sus términos números de Fibonacci. Si consideramos bn=un+1/un como el cociente de crecimiento, obtendremos una
sucesión, cuyo límite cuando n tiende a infinito es 1.618034...

Este número, juega un papel muy importante en la Geometría y en la Estética. Si dividimos un segmento de recta AB en un punto C tal que AB:AC=AC:CB tal división se llama sección o razón áurea (Kepler la llamó proporción divina). Si AB=1 y AC=x entonces x2+x-1=0. Luego x=.618034.... Así, la parte mayor de cualquier longitud, dividida en razón áurea, es igual a la longitud total multiplicada por .618034....

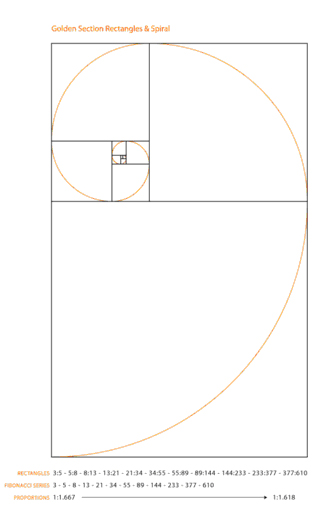
El número áureo, también denominado “número de oro”, “número dorado”, “sección áurea”, “razón áurea”, “razón dorada”, “media áurea”, “proporción áurea”, “divina proporción”, representado por la letra griega Φ (fi) (en honor al escultor griego Fidias), es el número irracional:

El número áureo en la Música

Autores como Bártok, Messiaen y Stockhausen, entre otros, compusieron obras cuyas unidades formales se relacionan (a propósito) con la sección áurea. También aparece en las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Debussý (estos compositores probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras).

Estudios realizados acerca de la Quinta sinfonía de Beethoven (1770-1827) muestran como el tema principal incluido a lo largo de la obra, está separado por un número de compases que pertenece a la sucesión. También en varias sonatas para piano de Mozart (1756-1791) la proporción entre el desarrollo del tema y su introducción es la más cercana posible a la razón áurea.

Relaciones matemáticas de este estilo se han encontrado también en la coral situada al final de Kunst der Fuge de Johann Sebastian Bach (1685-1750). En ella determinados motivos se repiten, por disminución a escalas menores, una y otra vez con distintas variaciones dentro de una región mayor de la pieza. Así, por ejemplo, varias voces repiten al doble de velocidad la melodía de la voz principal.

El compositor mexicano Silvestre Revueltas (1899-1945) utilizó también el número áureo en su obra Alcancías, para organizar las partes (unidades formales).

El grupo de rock progresivo norteamericano Tool, en su disco Lateralus (2001) hacen múltiples referencias al número áureo y a la secuencia Fibonacci, sobre todo en la canción que da nombre al disco, pues los versos de la misma están cantados de forma que el número de sílabas pronunciadas en cada uno van componiendo dicha secuencia. Además la voz entra en el minuto 1:37, que pasado al sistema decimal coincide muy aproximadamente con el número áureo.

Lateralus

Bartok

Béla Bartók (Nagyszentmiklós, Hungría -actualmente Sânnicolau Mare, Rumanía-, 25 de marzo de 1881- Nueva York, 26 de septiembre de 1945) fue un compositor, pianista e investigador de música folclórica de Europa del Este. Bartók fue uno de los fundadores del campo de la etnomusicología, el estudio de la música folclórica y la música de culturas no occidentales.

Bela Bartok, alrededor de 1915 desarrolló un método para integrar todos los elementos de la música (escalas, estructuras de acordes con los motivos melódicos apropiados, proporciones de longitud, tanto de la obra en general como los de la exposición, desarrollo, reexposición, frases de conexión entre movimientos etc.) basado en la razón áurea.

Bartok escribió que seguía a la naturaleza en la composición y que fue guiado indirectamente por fenómenos naturales para descubrir estas regularidades. Constantemente aumentaba su colección de plantas, insectos y especimenes minerales. El girasol era su planta favorita y se ponía muy feliz cuando encontraba piñas de abeto en su escritorio.

Consideraba que la música folclórica también era un fenómeno de la naturaleza y que sus formaciones se desarrollaban tan espontáneamente como otros organismos vivientes: las flores, los animales, etc. Por esto su música le recuerda al oyente de escenas naturales. Por ejemplo, el girasol tiene 34 pétalos y sus espirales tienen los valores 21, 34, 55, 89,144.

Su uso de los acordes también está basado en los números de Fibonacci. Por ejemplo, en semitonos, 2 es una segunda mayor, 3 es una tercera menor, 5 es una cuarta, 8 es una sexta menor y 13 es una octava aumentada, etc. Cuando Bartok utiliza acordes en un movimiento cromático, coloca la tercera menor sobre la cuarta justa de tal forma que el acorde adquiere la forma 8:5:3 y considerando una tercera menor, superponiéndole una cuarta seguida de otra tercera menor se obtiene su acorde característico mayor-menor.

El Allegro Bárbaro es otra composición para piano solo en la cual Bartok utiliza los números de Fibonacci 2, 3, 5, 8, y 13 en diversas ocasiones, a diferencia de la música tradicional la cual utiliza 8 compases en casi todos los temas y múltiplos de 2 en los motivos y frases. También utiliza su círculo de tonalidades y la duración de la pieza es de 3 minutos.

Allegro bárbaro

Conclusiones

Y bien, ¿qué relación existe entre la Música y la Matemática? Es decir, ¿qué conexión o correspondencia existe? Hemos visto cómo se han aplicado conceptos matemáticos (provenientes al fin y al cabo de la naturaleza, del pensamiento abstracto del Hombre, etc.) al entretenimiento con un juego de dados, a la Estética, a la Composición Musical y a la creación de un lenguaje preciso para la Musicología y la Música entre otros. Desde luego que la Acústica, la cual utiliza a la Matemática, es parte de la Física y de la Música.

Algunos piensan que la Matemática es un juego simple que sola y fríamente interesa al intelecto. Esto sería el olvidar la sensación de la belleza matemática, de la armonía de los números y las formas, así como de la elegancia geométrica. Esta es ciertamente una sensación de placer estético que todo verdadero matemático ha sentido y por supuesto que pertenece al campo de la emoción sensible. La belleza y la elegancia matemática consisten de todos los elementos dispuestos armónicamente tales que nuestra mente pueda abarcarlos totalmente sin esfuerzo y a la vez mantener sus detalles.

Esta armonía,es, de inmediato, una satisfacción de nuestras necesidades estéticas y una ayuda para la mente que sostiene y guía. Y al mismo tiempo, al poner bajo nuestra visión un todo bien ordenado, nos hace entrever una ley o verdad matemática. Esta es la sensibilidad estética que juega un papel de filtro delicado, la cual explica suficientemente el porqué el que
carece de ella nunca será un verdadero creador.

El genio de Mozart consistió en escoger las mejores o más bellas frases musicales de toda la enorme gama de posibilidades para crear su Música. La creación de nueva Matemática no consiste en hacer combinaciones nuevas de entidades matemáticas ya conocidas, sino solamente en tomar las combinaciones útiles, las cuales son una pequeña proporción. Si solamente fuera la rutina de aplicar reglas, las combinaciones obtenidas serían exageradamente numerosas, inútiles o extrañas.

Poincaré escribe a principios del siglo XX, que una demostración matemática no es una simple yuxtaposición de silogismos, sino silogismos colocados con cierto orden y que el orden en que son colocados es mucho más importante que los silogismos por sí solos. Comenta que no tiene miedo de que alguno de éstos se le olvide pues cada uno de ellos tomará su lugar en el arreglo sin el menor esfuerzo. También describe el proceso de creación [M]: primero se realiza un trabajo consciente acerca del problema, después deja madurar esas ideas en el subconsciente, luego aparece la solución, quizás cuando menos se espera, y finalmente ésta se escribe.

El Arte y la Ciencia son una actividad exclusivamente humana. Mucho más de la mitad del cultivo del conocimiento, es decir, de la cultura, lo constituye el conocimiento científico. Este es un hecho ampliamente ignorado por la mayoría de la gente que piensa que la cultura solamente está constituida por conocimientos literarios o artísticos. Es un gran error ver a la cultura de este modo.

Si en lugar de preguntarnos ¿qué relación existe entre la Música y la Matemática? Nos preguntáramos ¿qué relación existe entre los matemáticos y los músicos? Podríamos decir que algunos matemáticos adoran la Música, muchos con un enfoque similar a la medida estética de Birkhoff. A muchos matemáticos les agrada el orden mental, ven a la Música como si fueran matemáticas pero sin tener que lidiar con una lógica inflexible. Gustan más de
Mozart que de Stockhausen, Schoenberg o Bartok. Sin embargo a muchos músicos no les agrada la Matemática, generalmente por que no la conocen. Hay otros músicos a quienes sí les agrada la Matemática (Mozart, Bartok, Ponce, entre otros).

Si nos preguntamos más que cómo se relacionan, en qué se parecen, podría decir que, para los que ven a la Ciencia y al Arte como una actividad olímpica en donde se trata de ser altamente competitivos, productivos y pertenecer a las grandes ligas comerciales, la Matemática y la Música se utilizan como un medio y no como un fin. Así, algunos músicos se empeñan en tocar el mayor número de notas en el menor tiempo posible y ya se imaginarán ustedes el equivalente entre los matemáticos.

Recordemos que la ciencia y el arte son actividades esencialmente humanas. La Matemática es una de las "Bellas Artes" que posee el don de ser al mismo tiempo la más elaborada y sofisticada de todas las ciencias. Esta es una frase muy difícil de comprender para la mayoría de las personas. Sin embargo, la ciencia es una manera eficaz y elegante de comprender el universo. La ciencia se auto corrige. Nuestra vida y nuestro destino están indisolublemente ligados a la ciencia. Es esencial para nuestra simple supervivencia que comprendamos la ciencia. Para quien la comprende, la ciencia es un placer. Hemos evolucionado de tal modo que el hecho de comprender nos proporciona placer, porque el que comprende tiene mayores posibilidades de sobrevivir.

La Matemática, a diferencia de la Música, no es para espectadores. Es un lenguaje que, o bien se habla, o bien no se entiende absolutamente nada. No hay estadios de matemáticas para un gran público. Entonces, ¿qué relación existe entre la Matemática y la Música? J.J. Sylvester escribe en 1864: “May not Music be described as the Mathematic of Sense, Mathematics as Music of the reason? The soul of each the same?” Es decir, "¿Acaso no puede describirse la Música como la Matemática de lo sensible y la Matemática como la Música del entendimiento? El alma de cada una, la misma". Ambas se crean, se recrean, podemos apreciarlas y disfrutarlas. Una ventaja o desventaja, según se quiera ver, es que para la Matemática no existe un instrumento musical donde tocarla, ésta se queda a nivel de partitura, podría decir, que va directamente de pensamiento a pensamiento.

Se podría decir que la relación más importante entre la Matemática y la Música es, que ambas son "Bellas Artes". Poseen características similares. Están relacionadas en el sentido de que la Matemática provee una base científica para comprender la Música y la Musicología y para que esta última pueda considerarse una ciencia, no una rama de la literatura poética común y corriente.

Ya para acabar se podría establecer una vez más, que la Matemática es una de las "Bellas Artes", la más pura de ellas, que tiene el don de ser la más precisa y la precisión de las Ciencias.